板ばねを設計するうえで重要なことは、限られた容積の中で必要なばね荷重またはたわみを得るための形状の選定と、ばねに生ずる最大応力の位置と大きさの推定であるといえます。比較的簡単なばね形状に対しては一般の材料力学に示されている式が利用できますが、実際には様々な形状や使われ方があるため、ここでは形状別、用途別の薄板ばねの計算式をご紹介します。
– 目次 –
1 形状別の薄板ばね計算式
・1-1 長方形断面の片持ばね
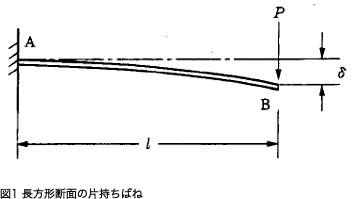
薄板ばねのもっとも単純なものは長方形断面の片持ちばねであるといえます。
固定端をA、自由端をBとして、点Bに荷重Pが加わった場合の計算式は
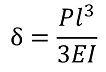
ここでIは断面2次モーメントを示します。
![]() であらわされ、
であらわされ、![]() が大きい場合には
が大きい場合には ![]() とします。
とします。
したがって、![]() が大きい場合の計算式は
が大きい場合の計算式は 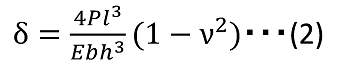 となります。
となります。
νはポアソン比をあらわし、鋼の場合、ν≒0.3である。応力は固定端で最大となり
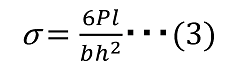 となります。
となります。
ここで主な薄板ばね材料の縦弾性係数Eの値を表2に示します。
表1. 計算に用いる記号及び単位
| 記号 | 記号の意味 | 単位 |
|---|---|---|
| h | 板厚 | mm |
| b | 板幅 | mm |
| l | 支点から荷重点までの距離 | mm |
| r | 円弧の半径 | mm |
| E | 縦弾性係数 | N/mm2 |
| I | 断面2次モーメント | mm4 |
| Z | 断面係数 | mm3 |
| P | ばねにかかる荷重(力) | N |
| δ | 荷重点のたわみ | mm |
| k | ばね定数 | N/mm |
| σ | 曲げ応力 | N/mm2 |
| ν | ポアソン比 | – |
表2.縦弾性係数:E(N/m㎡)
| 材料 | Eの値 | |
|---|---|---|
| ばね鋼鋼材 | 206×103 | |
| ステンレス鋼 | SUS301 SUS304 SUS631 |
186×103 186×103 196×103 |
| リン青銅 | 98×103 | |
| ベリリウム銅 | 127×103 | |
・1-2 台形状片持ちの薄板ばね計算式
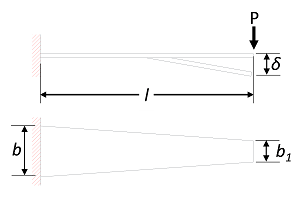
図2
図2にように、薄板ばねの板厚が一定で、板幅が直線的に変化している場合は、自由端のたわみ![]() は、
は、
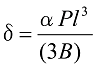
式4
式中のBの算出には、板厚によって以下の2種類の式を使い分けます。
板厚が厚い場合は、
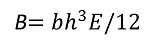
板厚がごく薄い厚い場合は、
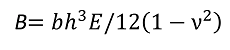
また、式中の![]() の値は、β=b1/bによって図3から求めます。
の値は、β=b1/bによって図3から求めます。
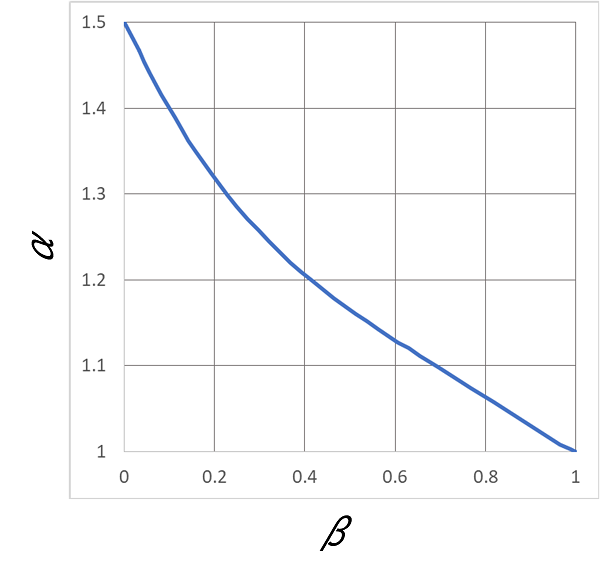
図3
・1-3 板幅が段付けをしている薄板ばね計算式

図4
図4のように、板厚が一定で、板幅が段付けをしている薄板ばねの自由端のたわみ![]() は、
は、

式5
ここで、![]() 、
、![]() はPによる段付き部Aのたわみとたわみ角、
はPによる段付き部Aのたわみとたわみ角、![]() は長さ
は長さ![]() 、板幅
、板幅![]() の片持ちはりの自由端のたわみを示します。
の片持ちはりの自由端のたわみを示します。
・1-4 円環状片持ちの薄板ばね計算式
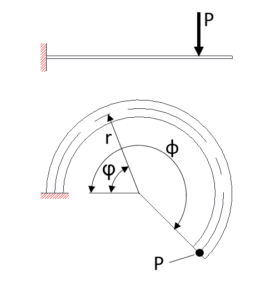
図5
板厚の中心が直線で、板幅の中心線が円弧状をしている図5のような形状に、垂直荷重Pが自由端に作用した場合、任意位置φでのたわみδφは、
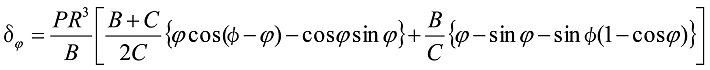
式6
となります。ここでCは板のねじり強さを表します。
・1-5 円弧状片持ちの薄板ばね計算式
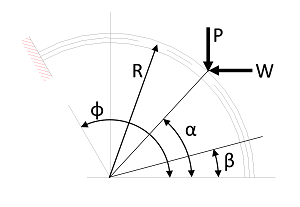
図6
板厚の中心線が円弧である片持ちばねに荷重が作用したときのたわみを求めるには、一般的にカスチリアノの定理を用います。以下にこの定理を利用した計算結果を示します。
図6に示す円弧状の薄板ばねに、垂直荷重P、水平荷重Wがそれぞれ単純に中心角![]() の位置に作用したとき、中心角
の位置に作用したとき、中心角![]() の位置でのy方向のたわみ
の位置でのy方向のたわみ![]() 、x方向のたわみ
、x方向のたわみ![]() は次のようになります。
は次のようになります。
Pによるたわみ![]() が、
が、
![]() のとき、
のとき、
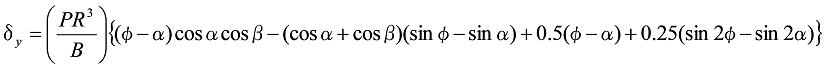
式7
![]() のとき、
のとき、
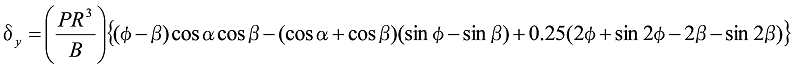
式8
Wによるたわみ![]() は
は
![]() のとき、
のとき、
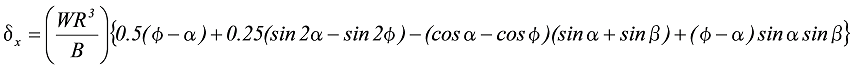
式9
![]() のとき、
のとき、
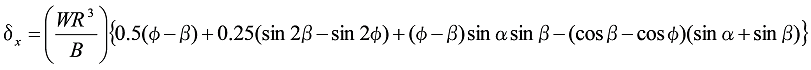
式10
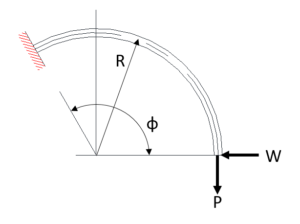
図7
図7においては、![]() 、
、![]() はそれぞれ次のようになります。
はそれぞれ次のようになります。
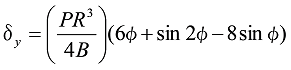
式11
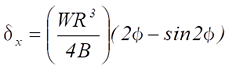
式12
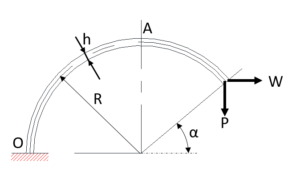
図8
図8の場合は、
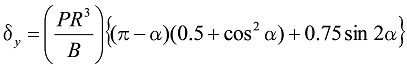
式13
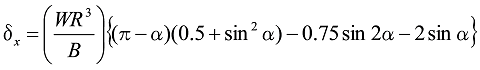
式14
となります。
Pによる最大応力![]() はつねに固定端に発生し、
はつねに固定端に発生し、
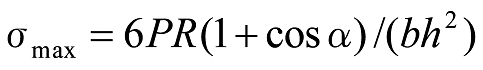
式15
Wによる最大応力は、![]() では図8のA点で、
では図8のA点で、![]() では固定端で起こり、
では固定端で起こり、
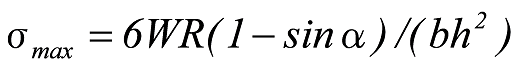
式16
となります。
・1-6 円輪状の薄板ばね計算式
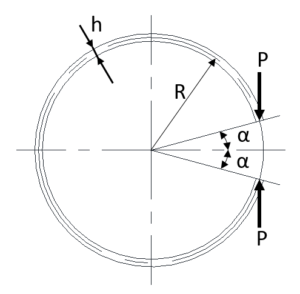
図9
図9に示す円輪状のばねは、上下対称であるので図8の形状のたわみの2倍が全たわみとなります。
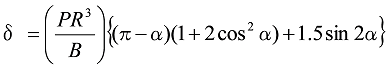
式17
・1-7 半円と1/4円との組み合わせの薄板ばねの計算式
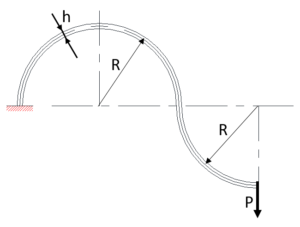
図10
図10に示す半円と1/4円との組合せの薄板ばねにおいては、
たわみは
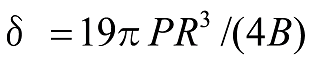
式18
最大応力は固定端に生じ、
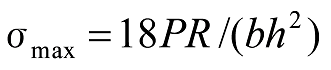
式19
となります。
・1-8 円弧の薄板ばねの計算式

図11
図11左側に示す形状の自由端のたわみは、
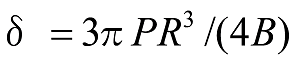
式20
図11右側の形状のように、水平方向が拘束されている円弧の場合は、

式21
で求められます。この二つの場合どちらも、最大応力は、
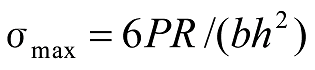
式22
で求められます。
・1-9 円弧と直線部を有する薄板ばねの計算式
・1-9-1 円弧と直線部を有する薄板ばねの計算式 その1
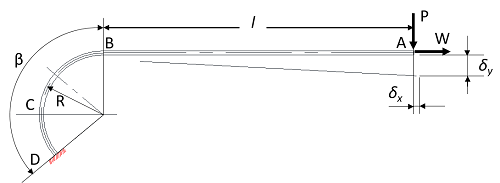
図12
図12のように、直線部ABと円弧部BDとが組合わせられて、一端Dが固定され、もう一端Aに垂直荷重Pまたは水平荷重Wが作用したとき、![]() 、
、![]() はそれぞれ次のようになります。
はそれぞれ次のようになります。
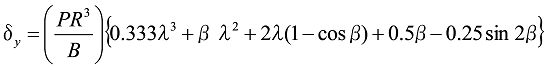
式23
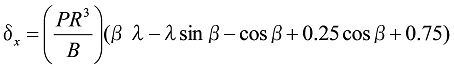
式24
![]() の場合には、
の場合には、
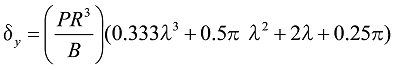
式C25
Wが作用する場合には、
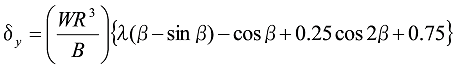
式26
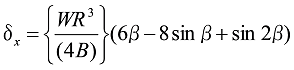
式27
となります。ここで、式中の![]() は、
は、![]() を表します。
を表します。
また、最大応力は、![]() では固定端において生じ、
では固定端において生じ、![]() ではC点に生じます。
ではC点に生じます。
・1-9-2 円弧と直線部を有する薄板ばねの計算式 その2
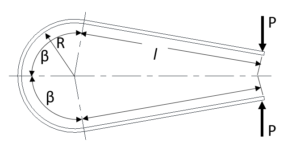
図13
図13のばねは、図12のばねを2つ組み合わせたもので、荷重作用方向のたわみ![]() は、式23で得られたたわみの
は、式23で得られたたわみの![]() 倍となります。
倍となります。
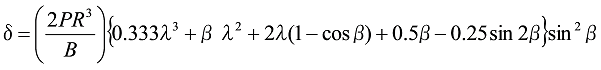
式28
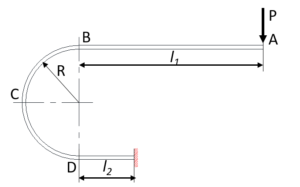
図14
図14のように、直線部と円弧部を有したばねのA端のたわみは、
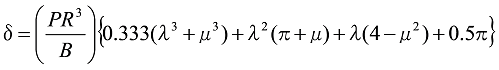
式29
ここで、![]() 、
、![]() を表します。
を表します。
最大曲げ応力は、C点において生じ、
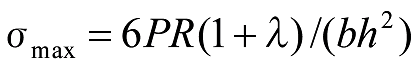
式30
となります。
![]() の場合は、
の場合は、![]() の場合、最大応力は固定端で起こり、
の場合、最大応力は固定端で起こり、![]() で
で![]() のときは、
のときは、
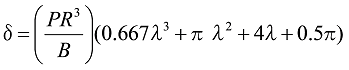
式31
となります。
・1-9-3 円弧と直線部を有する薄板ばねの計算式 その3
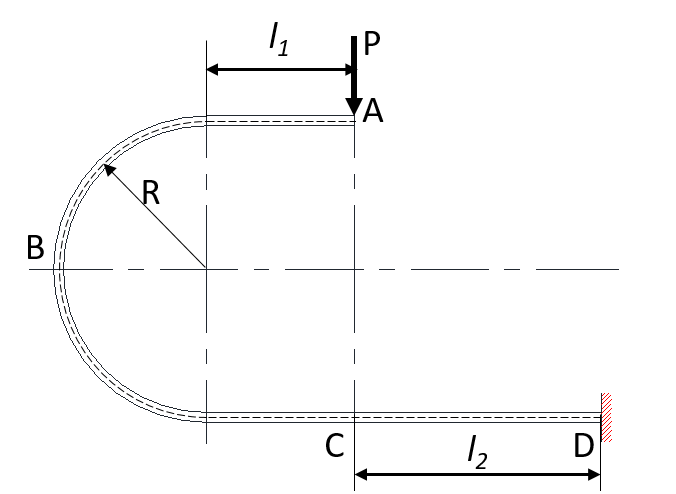
図15
図15の形状の場合には、AC部とCD部とを分割して、式25のたわみの2倍と式
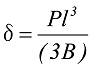
式32
のたわみをそれぞれ計算し、それらを合わせることでA部のたわみを得ることができます。
・1-9-4 円弧と直線部を有する薄板ばねの計算式 その4
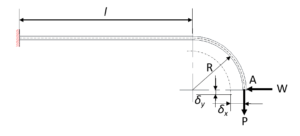
図16
図16のように、直線部が固定されており、円弧部のA端に荷重が作用したとき、A端垂直たわみ![]() 及び水平たわみ
及び水平たわみ![]() は、
は、![]() として荷重Pが作用したとき、
として荷重Pが作用したとき、
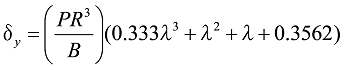
式33
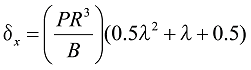
式34
となり、荷重Wが作用した場合は、
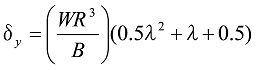
式35
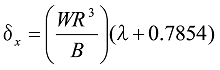
式36
となります。
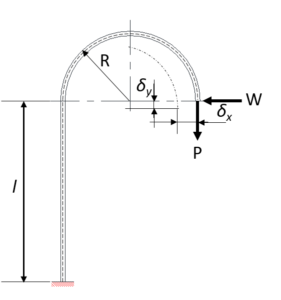
図17
図17の形状では、荷重Pが作用したとき、
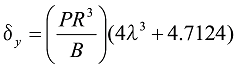
式37
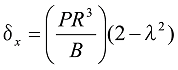
式38
となり、Wが作用した場合は、

式39

式40
となります。ここで、![]() を表します。
を表します。
・1-9-5 円弧と直線部を有する薄板ばねの計算式 その5

図18
曲率半径の小さい円弧と直線が組合わせれた図18のような形状のばねでは、円弧部の半径を無視してたわみは次式で表されます。
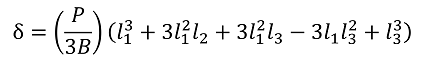
式41
最大応力は、![]() のとき、BC部に生じ、
のとき、BC部に生じ、

式42
![]() の場合は、固定端に生じ、
の場合は、固定端に生じ、
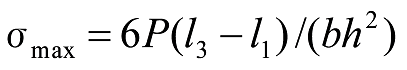
式43
となります。
・1-9-6 円弧と直線部が複雑に組み合わされる薄板ばねの計算式
薄板ばねの形状は、実際には円弧部と直線部が複雑に組み合わされたものが多く、これまでにご紹介した式を使用することができます。以下に示す形状と計算式はこれまでの応用的な考え方になります。
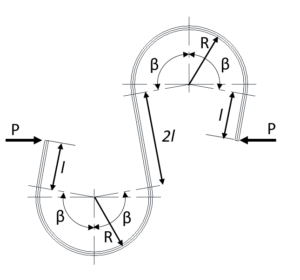
図19
図19の形状は、図13の形状が2個集まったものと考えて、式28の2倍としてたわみを求めることができます。
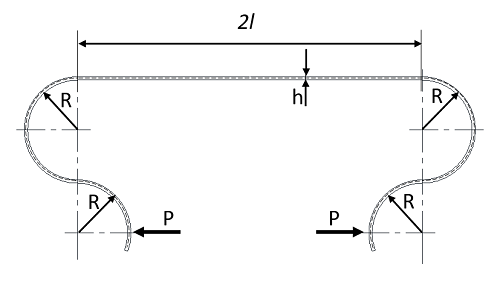
図20
図20の形状では、両端部が図10と同様であり、応力の式は式19で示すことができます。対称軸に関する片側のたわみは式18に![]() 部分を加えて、片側のたわみは、
部分を加えて、片側のたわみは、
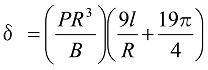
式44
が与えられます。
たわみ式は、
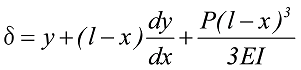
式45
で求められます。
2.特性・用途別の薄板ばね計算式
・2-1 非線形特性の薄板ばねの計算式
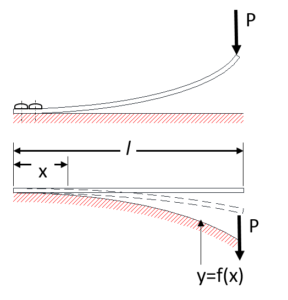
図21
非線形特性の薄板ばねは、図21のように、たわみによって、順次固定接着位置が変化するような接着部の構造にすると実現します。
非線形特性の薄板ばねの式は以下となります。
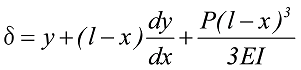
式46
・2-2 軸荷重と横荷重を受ける薄板ばねの計算式

図22
薄板ばねが図22のような荷重は、測定機器などの用途にみられます。一端が固定されて、もう一方の端は横方向に動けますが回転はできません。この場合は、軸荷重Pが座屈荷重に比べて小さいものとすると、横荷重Qによるたわみ![]() 及び応力
及び応力![]() は以下の式で表されます。
は以下の式で表されます。
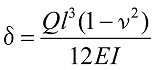
式47
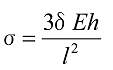
式48
Pが座屈荷重より大きい場合は、上の式に![]() によって決まる係数
によって決まる係数![]() 及び
及び![]() を乗じたものとなります。ここに、
を乗じたものとなります。ここに、![]() はオイラーの座屈荷重で
はオイラーの座屈荷重で![]() となります。ここで係数
となります。ここで係数![]() 、
、![]() は、以下の式となります。
は、以下の式となります。
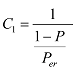
式49
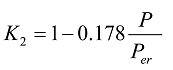
式50
・2-3 大たわみの薄板ばね計算式
・2-3-1 長方形断面の薄板ばね

図23
たわみが大きい場合、![]() は
は![]() に変化し、この影響を加味した計算結果を示したものが図24になります。
に変化し、この影響を加味した計算結果を示したものが図24になります。

図24
図の横軸は![]() を示し、縦軸は
を示し、縦軸は![]() 、
、![]() を示します。
を示します。![]() は板の曲げこわさを表し、
は板の曲げこわさを表し、![]() が大きいときには、
が大きいときには、![]() となります。図24を見ると明らかなように、
となります。図24を見ると明らかなように、![]() の値が小さい、つまり荷重Pが小さいときは、
の値が小さい、つまり荷重Pが小さいときは、![]() 及び
及び![]() は1に近く、
は1に近く、![]() の時に
の時に![]() 、
、![]() になります。したがって、この程度の変形の場合には、実用上大たわみとして取り扱わなくてもよいと考えられます。
になります。したがって、この程度の変形の場合には、実用上大たわみとして取り扱わなくてもよいと考えられます。
・2-3-2 台形状片持ちの薄板ばね
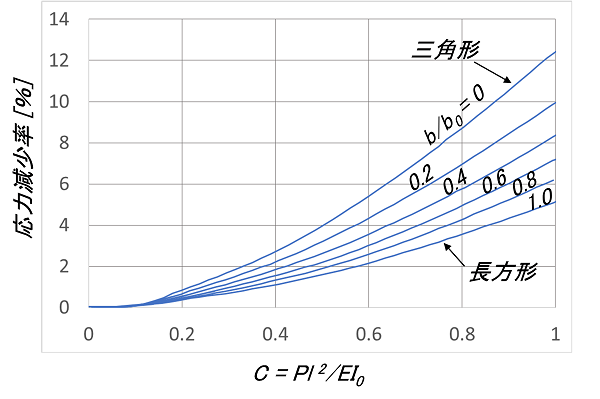
図25
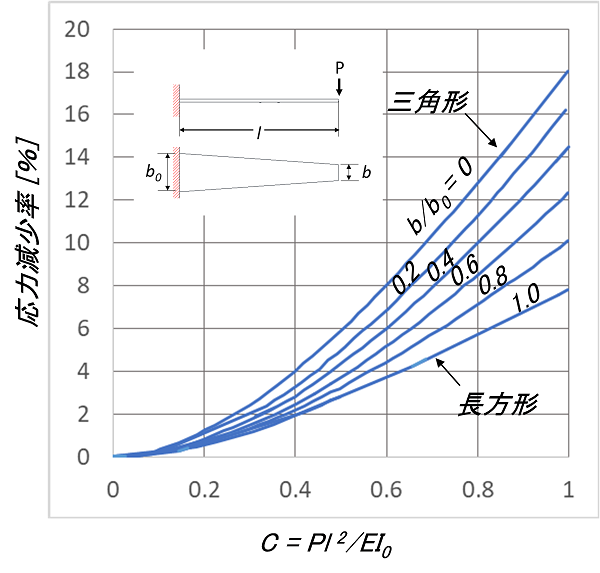
図26
台形状の片持ちの薄板ばねのたわみが大きい場合の近似値の結果を、図25、26に示します。横軸に![]() をとり、
をとり、![]() をパラメーターとして縦軸にはたわみまたは応力の減少率を示しており、これを式
をパラメーターとして縦軸にはたわみまたは応力の減少率を示しており、これを式![]() に適用すればよいということになります。
に適用すればよいということになります。



























![板ばねの導入事例[用途別]](/assets/images/products/leaf_top/side_2_ttl.png)